What are quantum computers?
If you are not expert in quantum computing (yet), you can learn some of the basics with us. Having a grasp of key concepts and terms can help you make sense of the news in the field.
An important takeaway: quantum computers are not just faster versions of today’s computers. By encoding information in quantum states, quantum computers gain access to ways of processing information that are not available to classical computers operating on binary bits. Quantum algorithms and quantum simulations can exploit these features to solve problems other computers find hard.
What follows is a beginner’s guide to quantum hardware. We will be expanding this section, and we invite you contact us with your feedback and questions you’d like us to answer next.
To learn about more topics in more depth, you can enrol in free online courses at our training platform qutalent.org.
The basics
Meet the qubit
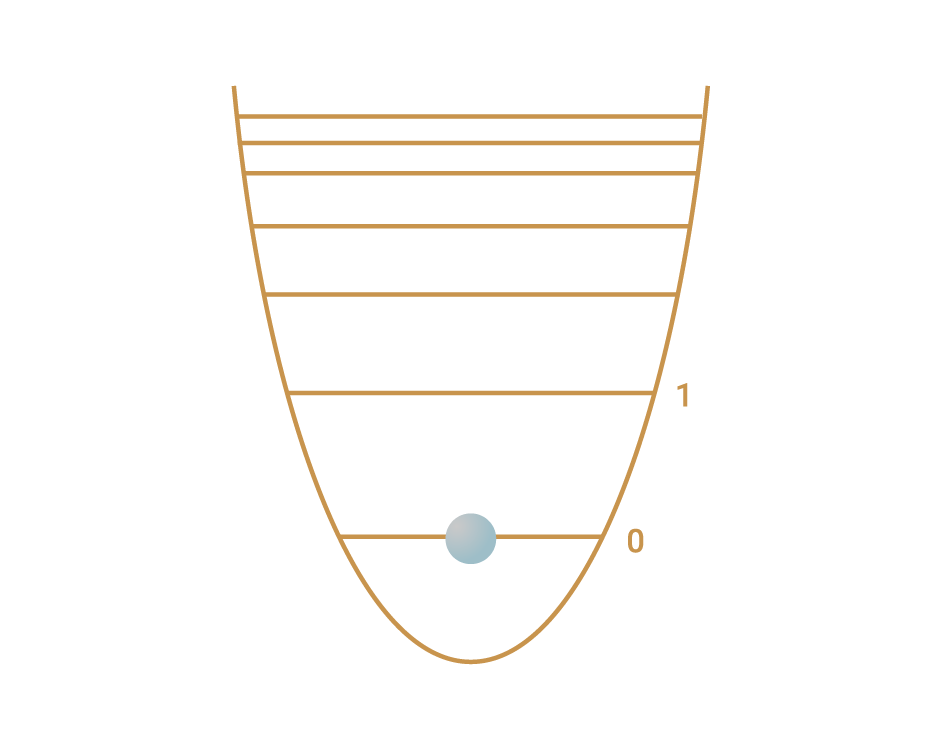

The angles show superposition and phase
- A qubit is the quantum version of a classical bit and it is encoded in a two-level quantum system.
- The high and low energy states represent one and zero. A qubit is often shown with a Bloch sphere representation.
- A qubit’s 1 and 0 have the possibility of existing in a superposition. The qubit can also carry phase information.
- These features are key in quantum computing because they create both new ways of storing information and of processing it. Entanglement is often cited too: this is a superposition spread across the states of two or more qubits.
- To understand how qubits can be realised in different physical systems, check the qubit intros below.
Superconducting qubits are circuits manufactured with microelectronic techniques.
They contain structures called ‘Josephson junctions’ that create the conditions for a two-level system.
They must operate at close to absolute zero, around 10 milliKelvin, in special dilution refrigerators.
There are two designs of superconducting qubits – fixed frequency and tunable frequency.
Tunable frequency qubits are more prone to noise but have faster gate times.
Fixed frequency qubits have higher coherence times but slower two-qubit gates.
Neutral atom qubits are encoded in two energy levels of an atom. As all atoms of a given species are identical by nature, the qubits are also identical and do not required sophisticated fabrication procedures.
Atoms are cooled with laser light and trapped using optical tweezers. Since optical tweezers do not require high power, hundreds or more traps can be operated simultaneously.
Generally, qubits are encoded in long-lived states, well-protected from their environment. Sometimes, one needs to open this coupling to let the qubits interact with each other. This operation is done for a very short time, transporting one qubit state to a highly excited state called a Rydberg state. This enables two-qubit gates.
Solid state qubits exploit the inherent quantum nature of particles (e.g. atoms, electrons) in solids by engineering controls to isolate, manipulate and read-out the qubits.
They can be optically or electrically addressed.
The optically addressable qubits can work at room temperature, while the electrically addressed ones typically require temperatures less than 100 milliKelvin to operate (although recent candidates have shown ability to work at temperatures up to 1 Kelvin).
Solid state qubits hold promise for scaling up to large numbers, but the current challenge is to engineer these qubits reproducibly in scalable processes.
Trapped ions are charged atoms that are confined in a space using electromagnetic fields.
Information is encoded in the quantum states of these ions, specifically in their internal energy levels.
Trapped ions are appealing for quantum computing due to their quantum states having long coherence times and a high degree of controllability with lasers and microwaves.
Operations can be performed at high fidelity.
A significant challenge is the necessity for precise control over individual ions within a trap, as any unwanted interaction or disturbance can lead to errors in computation.
Photons hardly interact with each other. This makes them suitable as long-lived flying qubits in quantum computing.
In quantum information, photons can encode information in two ways: in discrete and continuous variables.
Discrete variable qubits rely on single photon sources and encode information in properties such as a photon’s polarisations or path (in dual rail encoding).
Continuous variable qubits use the wave nature of photons to encode information in properties like frequency or quadratures.
Implementing quantum gates with photons is challenging due to their weak interaction with each other.
With integrated photonics, the technology for optical quantum computing can be miniaturised on chips.
Nitrogen-Vacancy (NV) centres consist of a nitrogen atom that has replaced a carbon atom in a diamond lattice and an adjacent vacancy.
Qubit information is encoded in the NV centres’ electronic ground state spins and nuclear spins.
NV centres can convert magnetic and electric field noise into optical signals at room temperature, which enables very sensitive readout, achieving nanoscale resolution.
Significant challenges are scaling the number of qubits and integrating with existing technologies while retaining the distinctive properties of NV centres.
The computing paradigms
Gate based – a universal computer that can run any programme written as a series of logic gate operations.
Analogue – annealing finds an energy minimum, solving problems that can be converted into an energy minimisation task.
Measurement-based – a one-way computer that takes a large entangled state as the input.
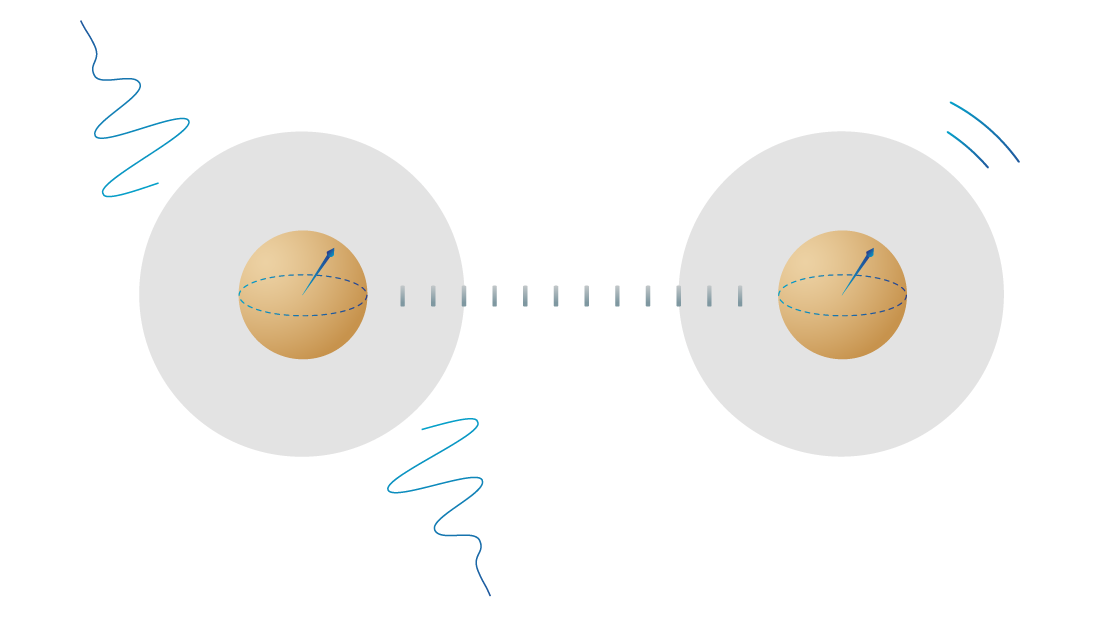
The challenge
You have two opposing needs:
- To protect the quantum state from outside influences that change it, introducing ‘noise’ or errors in your computation.
- To operate on the quantum states to process information, using outside influences to control the qubits’ interactions.
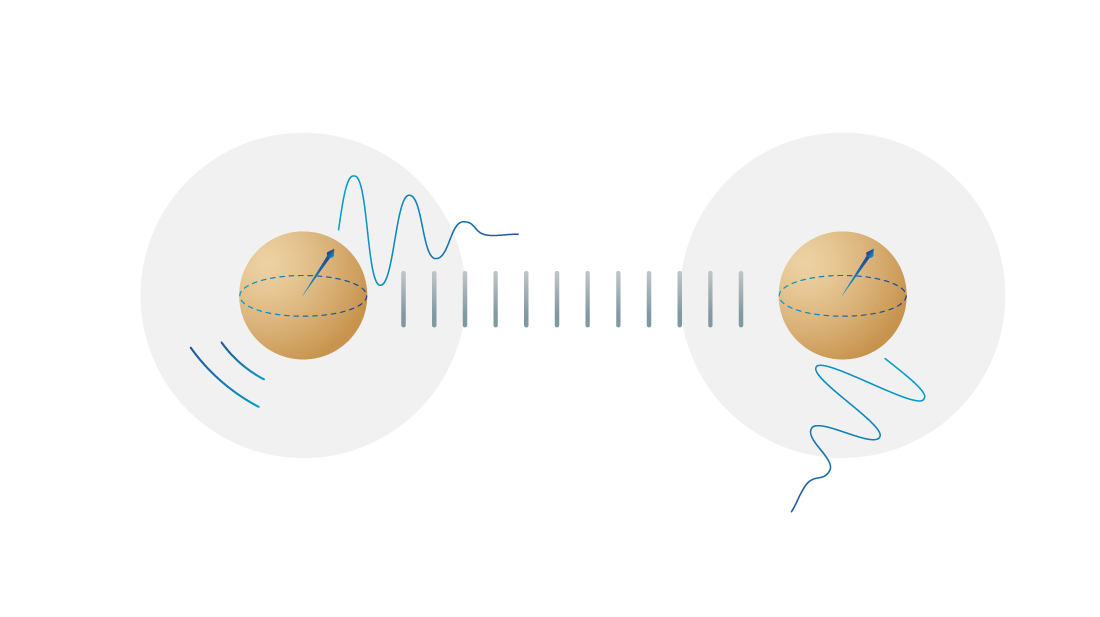
Elementary gates
Gates are the building blocks for algorithms you run on the quantum computer:
- To operate on one qubit to change state or phase.
- To operate on multiple qubits.
Some examples that together are universal (meaning that together they can perform any operations):
- CNOT – control not, flip the target qubit based on the state of the control qubit.
- Single qubit gates – Pauli X, Y, Z
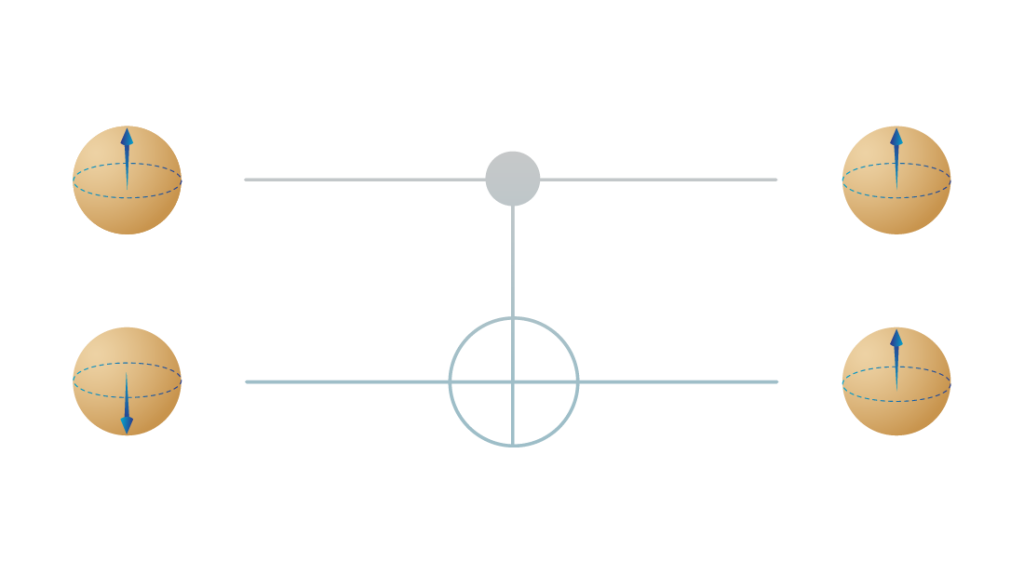
The qubits' initial states are shown on the left and final states on the right.
Types of errors

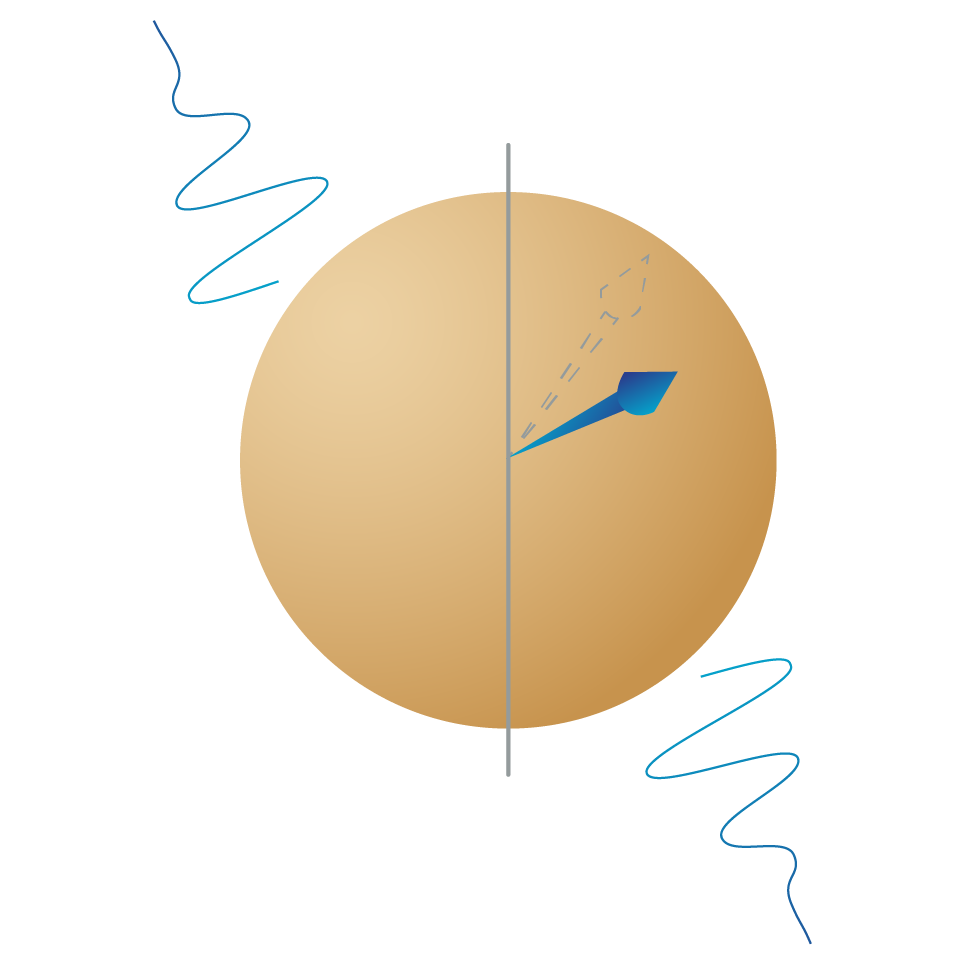
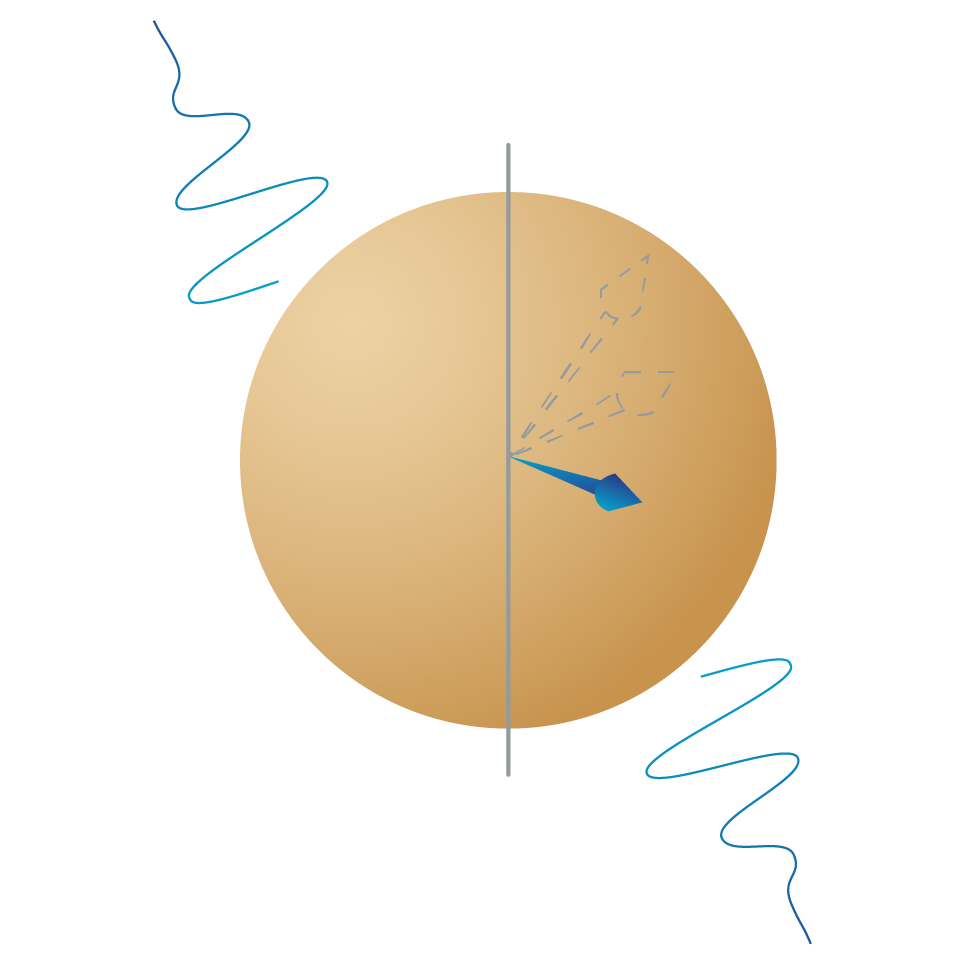
When the state of a qubit differs from its expected state, the culprit is noise. The term NISQ often used to describe quantum computers stands for “noisy intermediate-scale quantum” and means noise is uncorrected in the device. Sources of noise include:
Decoherence: the collapse of superpositions, or more technically non-unitary evolution, resulting from a qubit’s interaction with the environment.
Imperfect gates: when operations performed on the qubit don’t exactly match specifications.
Crosstalk: qubits are affected by the states of each other and are influenced by operations performed on other qubits. Managing such crosstalk is a big challenge for scaling to larger number of qubits.
The baseline metrics
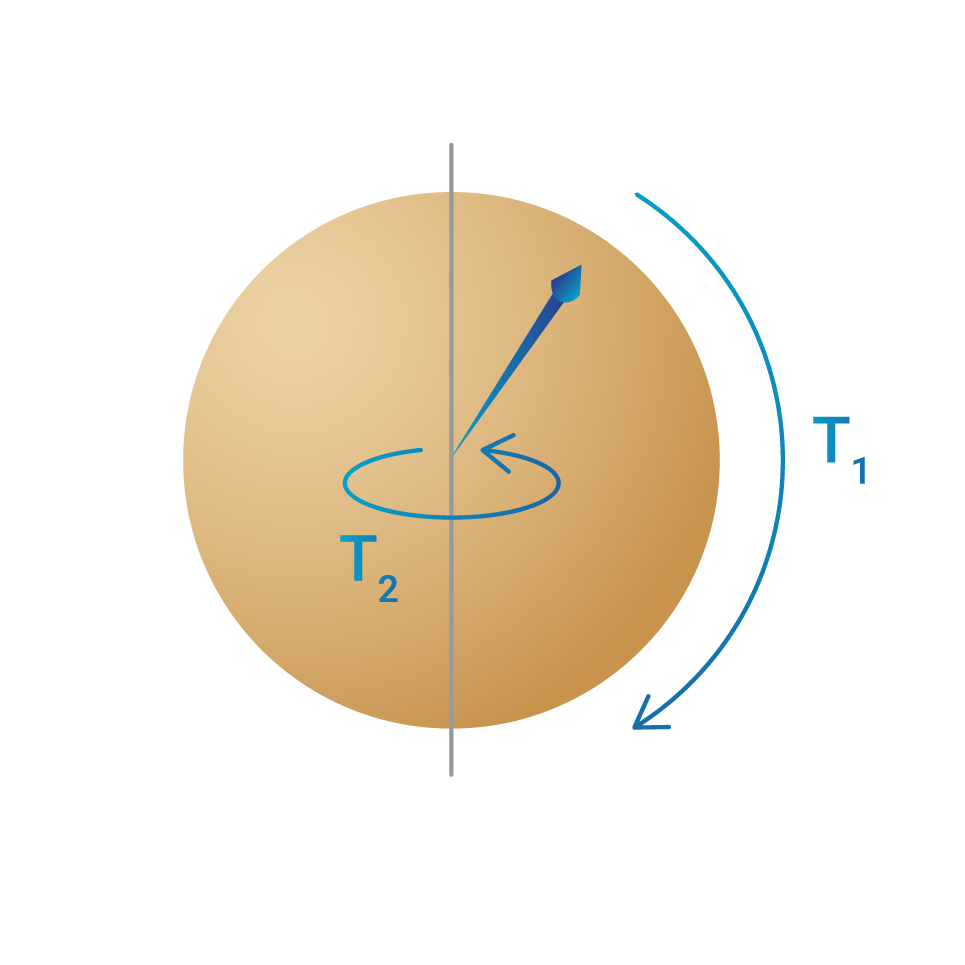
You measure the stability of a qubit – its robustness – with coherences times. The longer the coherence time, the better.
- T1 = how quickly a one changes to a zero.
- T2 = how quickly phase information decays.
Your ease of performing gates is captured in the gate speed.
The fidelity of your gate is how likely the gate operation is to deliver the intended outcome – a typical target is ‘four nines’, meaning 99.99%.
The ratio of coherence time to gate time approximately tells you the achievable circuit depth – how many layers of operations you can perform within the qubit’s lifetime.
The error-corrected future
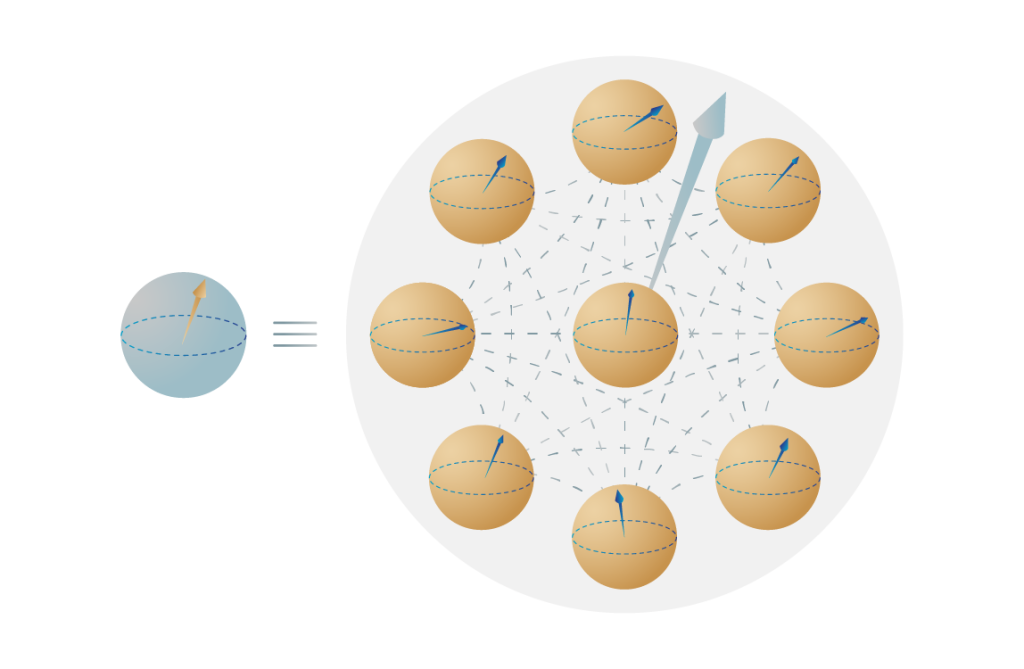
- Error correction is a technique to extend the effective coherence time of qubits.
- One ‘logical qubit’ is created from many physical qubits with a code operating on them to erase errors as they arise. The logical qubit has a longer effective coherence time than the individual physical qubits.
- Different error correcting codes exist.
- Error mitigation measures may also help reduce noise.
Beyond counting qubits
- Counting qubits is not enough to tell you the power of your quantum computer because of the impact of noise.
- Quantum volume considers both qubit count and coherence times, multiplying the number of qubits by the achievable circuit depth.
- More useful is the count of logical qubits, meaning the number of error-corrected qubits you create from your physical qubits. The largest number of logical qubits reported so far is 48.
- Another measure is algorithmic qubits. This tells you, for a specific algorithm and noisiness, how many logical qubits you can use for computation. It takes into account whether the algorithm will return an accurate result, known as the result fidelity.
- There are other methods to measure performance too. One approach is randomised benchmarking: this is a test checking if qubits go back to their original state after a cycle of a particular kind of gate called Clifford gates (U†U).
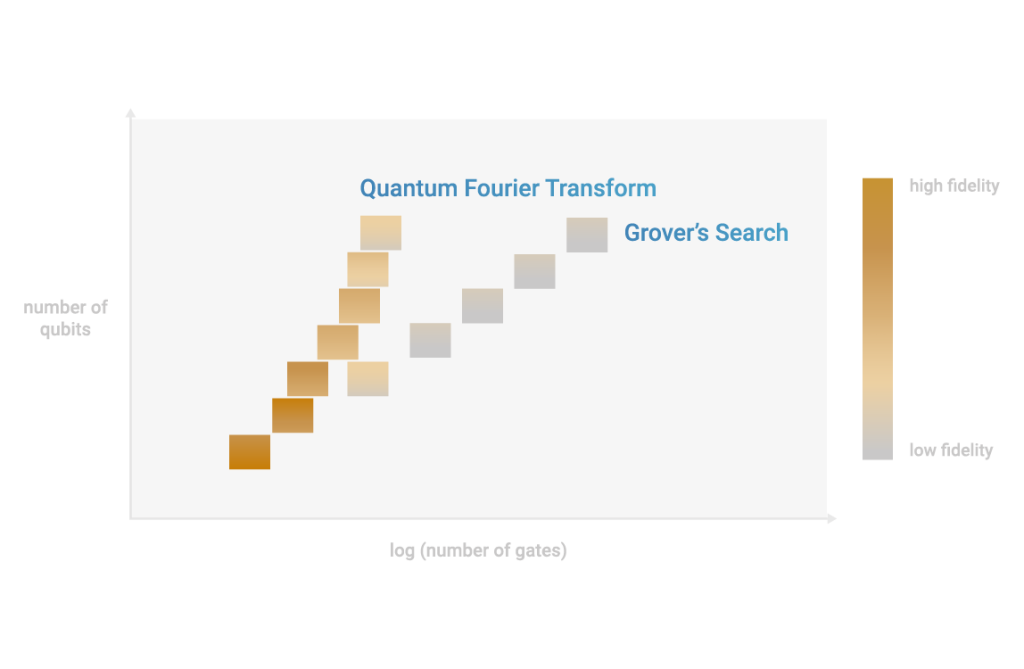
What algorithms exist?
Not every computation can run faster or in parallel on a quantum computer. Only certain algorithms are known to bring advantages. Known algorithms offering a speedup mostly rest on a few primitives:
- Grover
- HHL for linear systems
- Networks of harmonic oscillators
- Quantum Fourier Transform
More algorithms are listed at quantumalgorithmzoo.org
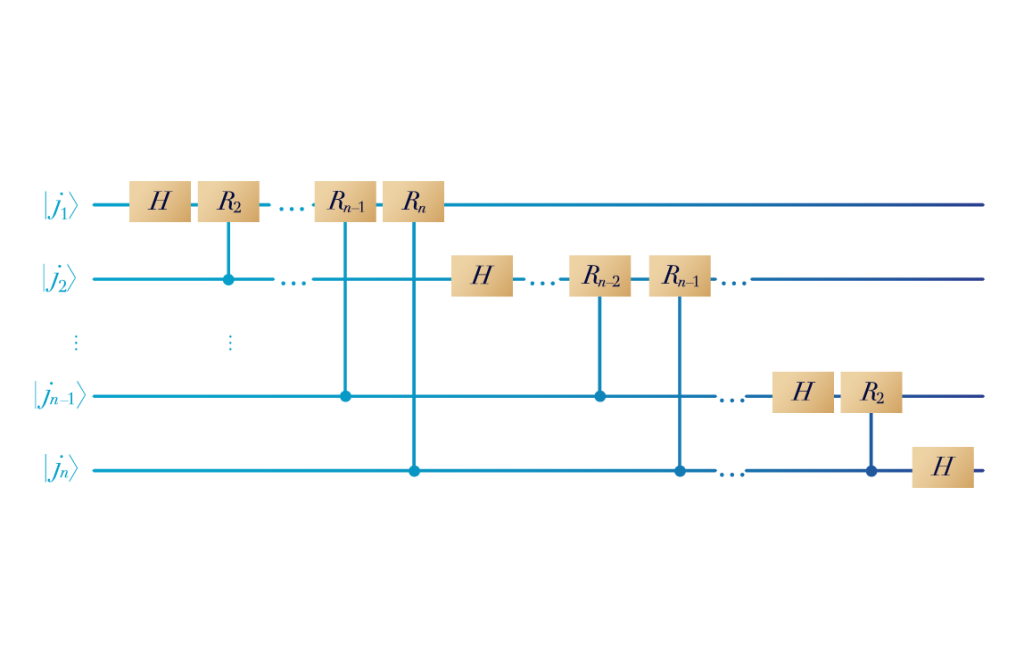
Making algorithms efficient
- Qubit encoding schemes can make more efficient use of a limited number of qubits.
- Algorithms operate on data encoded in quantum states. The encoding of data is also known as the QRAM problem.
- We can explore encodings that allow us to pack more information into a single qubit.
- Encoding can make more efficient use of physical hardware.
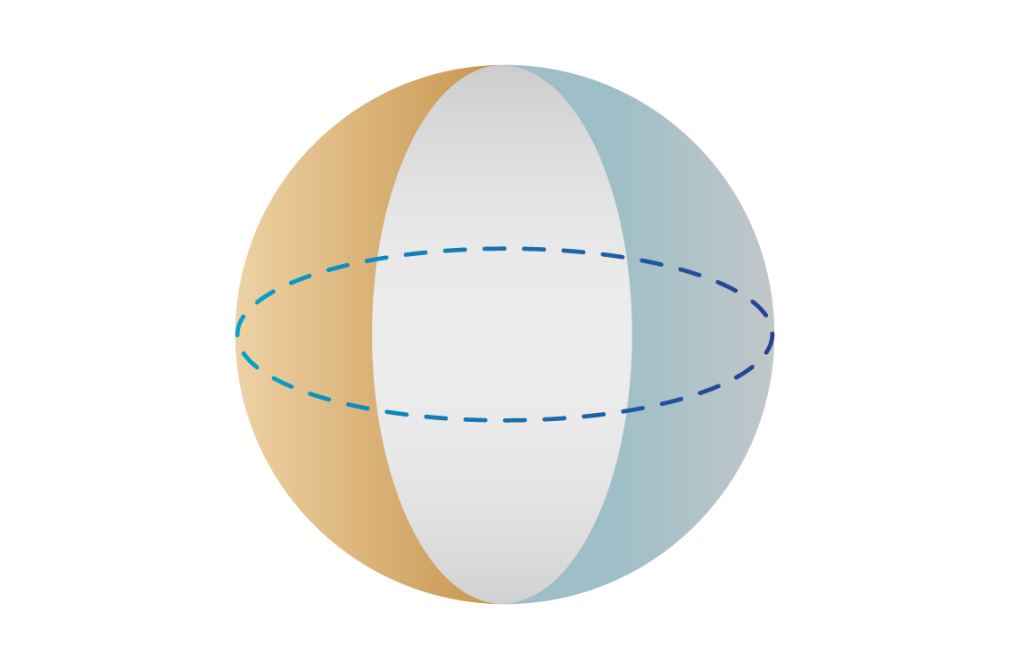
- Options might include encodings in the quadrants of a Bloch sphere, or in correlations among groups of qubits.
What else to know
- A challenge for practical quantum computing is how to get data into the system. You have to initialise the machine by converting classical data into quantum states.
- Quantum computing is not the solution to all problems. Known algorithms so far can offer improvements for a limited, albeit important, set of calculations.
- The design of quantum memory is still a work in progress.
- Quantum algorithms are often probabilistic, meaning you’ll need to run them multiple times to find the best answer.
- Quantum simulation is something different: it doesn’t necessarily use gates or need error correcting codes, instead arranging qubits to mimic the system of interest, such as a material or network.
- Quantum computers may be used together with digital computers as ‘accelerators’ for certain types of calculation. These setups are described as hybrid.




